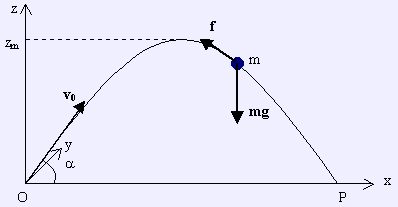f : Frottement fluide f : ( fx , fy , fz ) mg : Poids du mobile mg : ( 0 , 0 , -mg ) v0 : Vitesse initiale v0 : ( v0 cos α, 0 , v0 sin α ) z0  :  Altitude initiale α :   Angle initial de lancement OP : Portée du lancer zm  : Flèche du lancer

ma = mg + f    donc  a = g + f/m

Remarque : Si on veut tenir compte de la poussée d'Archimède F_A = ρ₀ V g₀ , on peut l'intégrer dans g :
mg = mg₀ - F_A = ρ V g₀ - ρ₀ V g₀ = ρ Vg₀ (1 - ρ₀/ρ) = mg₀ (1 - ρ₀/ρ)
g = g₀ (1 - ρ₀/ρ)                 ( ρ₀ est la masse volumique du fluide, ρ est celle du mobile et g₀ est l'intensité de la pesanteur )

En projection sur les trois axes, on obtient :
a_x = f_x/m

a_y = f_y/m = 0

a_z = - g + f_z/m

a_y = 0 donc v_y = constante. A t = 0, v_y = v_0y = 0 donc v_y = 0 à tout instant.
v_y = 0 donc y = constante.
y = constante donc le mouvement est plan, il se maintient dans le plan x O z

3.1 Équations horaires du mouvement

On néglige le frottement f ( Objet dense à vitesse faible ou mouvement dans le vide )
a_x = 0 => dv_x/dt = 0 => v_x = constante
A t = 0, v_x = v_0x = v₀ cos α, donc v_x = v₀ cos α  
v_x = v₀ cos α = dx/dt  => x = v₀ cos α t + x₀     ( On prend  x₀ = 0 )
   x = v₀ cos αt

a_z = - g => dv_z/dt = - g => v_z = - g t + K
A t = 0, v_z = K, or à t = 0, v_z = v_0z = v₀ sin α, donc v_z = - g t  + v₀ sin α 
v_z = - g t  + v₀ sin α = dz/dt  => z  = -1/2 g t²  + v₀ sin α t + z₀
A t = 0, z = z₀
   z  = - 1/2 g t²  + v₀ sin α t + z₀

3.2 Équation du mouvement

x = v₀ cos α t
z  = -1/2 g t²  + v₀ sin α t 
t  =  x/ ( v₀ cos α)
z  = -1/2 g (x/ (v₀ cos α))²  + v₀ sin α x/ (v₀ cos α) + z₀ =  -1/2 g x²/ (v₀² cos² α ) +  tan α x + z₀ 
    z  = - 1/2 g x²/ (v₀² cos² α)  +  tan α x  + z₀     Équation d'une parabole

3.3 Flèche ( altitude maximum )

z  =  z _max quand dz/dx = 0
dz/dx = - g x/(v₀² cos² α ) +  tan α = 0
x  = tan α v₀² cos² α /g = v₀² cos α sin α /g
z_max = -1/2 g (v₀² cos α sin α /g)²/ (v₀² cos² α ) +  tan α v₀² cos α sin α /g + z₀ 
z_max = -1/2 v₀² sin² α /g+  v₀² sin² α /g  =  v₀² sin² α /2g + z₀ 
   z_max = v₀² sin² α /2g + z₀ 

3.4 Portée du lancer pour  z₀ = 0

En P, z = 0 donc z  =  -1/2 g x²/ (v₀² cos² α)  +  tan α x  = 0
donc  -1/2 g x/ (v₀² cos² α)  +  tan α  = 0  => x =  2 tan α (v₀² cos² α) /g
   x = 2 v₀² sin α cos α /g

Angle α_m le plus favorable :
x est maximum  si dx/dα = 0
donc si  2 v₀²/g(cos² α_m  -  sin² α_m) = 0   => cos² α_m  -  sin² α_m = 0
cos² α_m  -  sin² α_m  = 1 - 2 sin² α_m = 0     => sin² α_m = 1/2   =>   sin α_m = 1/2^1/2
  α_m = 45°

3.5 Parabole de sûreté

La parabole de sûreté est l'enveloppe parabolique de toutes les trajectoires possibles pour une vitesse initiale donnée.
En dehors de cette parabole, un objet ne peut être atteint.

Cette parabole part horizontalement de l'altitude maximale atteinte à la verticale ( α = 90° )  z_max =   z₀ + v₀²/(2g)   et descend tangentiellement à toutes les trajectoires. Son équation est donc z =  z₀ + v₀²/(2g) - a x²

A point de tangence, les deux paraboles se "coupent" en un seul point, donc 
  z₀ + v₀²/2g  - a x² = -1/2 g x²/(v₀²cos² α) +  tan α x + z₀ 
x²(a - g/(2v₀²cos² α))  +  tan α x - v₀²/(2g) = 0
Cette équation n'a qu'une solution si le discriminant est nul donc si
tan² α + 2a v₀²/g  - 1/cos² α = 0      ou    2a v₀²/g = 1/cos² α - sin² α/cos² α  = 1
a = g/(2v₀²)     Le coefficient est indépendant de α  donc la parabole est bien tangente à toutes les trajectoires si α >= 0
L'équation de la parabole de sûreté est donc :

z = z₀  + v₀²/(2g) - g/(2v₀²)  x²

Accessoirement, le contact se fait en x = v₀²/(g tan α)           (   x >= 0 donc α >= 0  )

4. Étude du mouvement avec frottement fluide laminaire

4.1 Équations horaires du mouvement

Si le frottement est quelconque, on ne peut obtenir de solutions algébriques, il faut faire une étude numérique. Cependant dans le cas du frottement fluide laminaire  
f = - k v, on peut obtenir les solutions algébriques
( Pour un frottement turbulent,  f = - k v v, on peut prendre k v constante en remplaçant v par une vitesse moyenne adaptée. L'expérience montre qu'une valeur  0,9 v₀ >  v_moy  > 0,7 v₀ donne de bons résultats jusqu'à des vitesses importantes, des angles de tir pas trop grands et des coefficients de frottement raisonnables )

a_x = f_x/m = - kv_x/m  => dv_x/dt = - hv_x   => dv_x/dt + hv_x = 0      ( h = k/m )
Équation différentielle de premier ordre dont la solution est du type v_x = A e ^{- ht}
A t = 0, v_x = A e ^{- ht}  = v_0x = v₀ cos α,  donc A = v₀ cos α
v_x = v₀ cos α e ^{- ht}  = dx/dt  => x = - v₀ cos α /h  e ^{- ht}  + B
A t = 0, x = 0 = - v₀ /h cos α  + B, donc B = v₀ cos α/h 
  x  =  v₀ cos α /h (1 - e ^{- ht} )    

a_z = - g - hv_z => dv_z/dt = - g - hv_z   => dv_z/dt + hv_z = - g
Équation différentielle de premier ordre dont la solution est du type v_z = A e ^{- ht} - g/h
A t = 0, v_z = A - g/h, or à t = 0, v_z = v_0z = v₀ sin α, donc A = v_z =  g/h  + v₀ sin α
v_z = ( g/h  + v₀ sin α) e ^{- ht} - g/h  = dz/dt  => z  = - ( g/h²  + v₀ sin α/h ) e ^{- ht} - g/h t + B
A t = 0, z = z₀ = - ( g/h²  + v₀ sin α/h )+ B, donc B = ( g/h²  + v₀ sin α/h ) + z₀ 
   z  = ( g/h²  + v₀ sinα/h ) (1- e ^{- ht} )  -  g/h t  +  z₀ 

4.2 Équation du mouvement

x  =  v₀ cos α /h (1 - e ^{- ht} )  =>  (1 - e ^{- ht} )  = h x/(v₀ cos α)
e ^{- ht}   =  1 - h x/(v₀ cos α )=>  -ht = log_e( 1 - h x/(v₀ cos α)) => t = -1/h log_e( 1 - h x/(v₀ cos α)) 
z  = ( g/h²  + v₀ sin α/h ) h x/(v₀ cos α) +  g_/h² log_e( 1 - h x/(v₀ cos α)) + z₀ 
  z  = ( g/( hv₀ cos α )  + tan α) x  +  g/h²  log_e( 1 - h x/(v₀ cos α)) +  z₀

4.3 Flèche ( altitude maximum )

On pose : u = h/(v₀ cos α)  x
z  = ( g/( hv₀ cos α )  + tan α ) u (v₀ cos α) /h  +  g/h²  log_e(1 - u ) + z ₀ 
z  = ( g/h²  + v₀ sin α /h) u  +  g/h²  log_e(1 - u ) + z ₀ 
z = g/h² ((1  + h v₀ sin α /g)  u  +  log_e(1 - u )) + z ₀ 
On pose a = 1  + h v₀ sin α /g
z = g/h² ( a u  +  log_e( 1 - u )) + z ₀ 
z  =  z _max quand dz/du = 0
dz/du = g/h² ( a  - 1/( 1 - u )) = 0 =>  1 - u = 1/a => u = 1 - 1/a = (a -1)/a
donc  z_max =  g/h² ( a -1  +  log_e(1/a )) + z ₀ = g/h² ( h v₀ sin α /g  +  log_e( 1/(1  + h v₀ sin α /g ))) + z ₀ 
   z_max =  v₀ sin α /h + g/h²  log_e( 1/(1 + h v₀ sin α /g )) +  z ₀

4.4 Portée du lancer

z = g/h² ( a u  +  log_e( 1 - u )) + z ₀      avec    a = 1  + h v₀ sin α /g     et     u = h/(v₀ cos α)  x 
En P, z = 0 donc  g/h² ( a u  +  log_e(1 - u )) + z₀  = 0 => a u  +  log_e(1 - u ) = - b     avec   b = z ₀ h²/g
log_e (1 - u ) = - a u - b  =>  1 - u = e ^{- ( au + b )}  =>  u = 1 - e ^{- ( au +  b )}